NPV of Project: Decide Whether To Do Or Not To Do A Project

NPV Of Project Explained With Example

In the world of finance, net present value (NPV) is a crucial metric used to evaluate the profitability of potential investments or projects. It essentially determines whether a project is worth pursuing based on its expected future cash flows. However, NPV can sometimes be perceived as a complex concept, especially for those unfamiliar with financial jargon.

To make NPV more approachable, let’s consider a simplified example of a project with an initial investment and expected cash flows over the next 10 years.

Project Overview

Imagine you’re considering investing in a new coffee shop venture. The initial investment for setting up the shop, purchasing equipment, and securing a lease is estimated to be $50,000. Based on market research and projections, you anticipate generating the following cash flows throughout the first 10 years:

Year 1: $20,000
Year 2: $30,000
Year 3: $40,000
Year 4: $35,000
Year 5: $40,000
Year 6: $50,000
Year 7: $55,000
Year 8: $45,000
Year 9: $50,000
Year 10: $60,000

Calculating Net Present Value (NPV)

While the expected cash flows over the project’s lifetime provide insights into its potential profitability, they don’t fully reflect the value of those cash flows today. This is because the value of money changes over time due to factors like inflation. To account for this time value of money, we use a discount rate, which represents the expected rate of return for comparable investments.

In our coffee shop example, let’s assume a discount rate of 10%. This means that for every dollar received in the future, it is worth less today (by 10% per year). To calculate the present value of each cash flow, we use the following formula:

Present Value = Future Cash Flow / (1 + Discount Rate) ^ Year

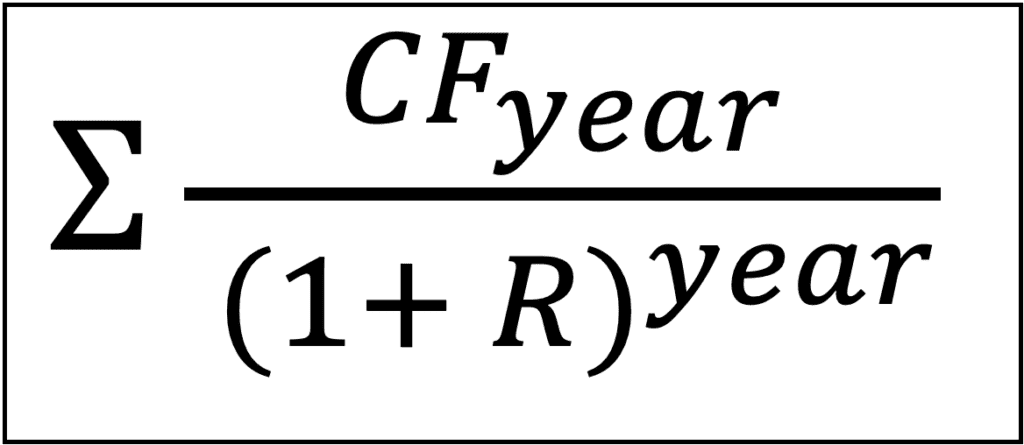
For instance, the present value of the first year’s cash flow ($20,000) would be:

Present Value = $20,000 / (1 + 0.10)^1 = $18,181.82

the present value of the second year’s cash flow ($30,000) would be:

Present Value = $30,000 / (1 + 0.10)^2 = $24,793.39

We follow the same approach for all the future 10 years to compute the total present value of all future cash flows.

Now, to calculate the NPV, we simply subtract the initial investment from the sum of all the present values:

NPV = Sum of Present Values – Initial Investment

Use NPV Calculator to Calculate NPV of Project

The NPV of project ‘Cafe’ can be calculated easily using the NPV Calculator in 4 steps.

Step 1. Open the NPV Calculator Page

Or you can use the NPV Calculator app on the iOS store.

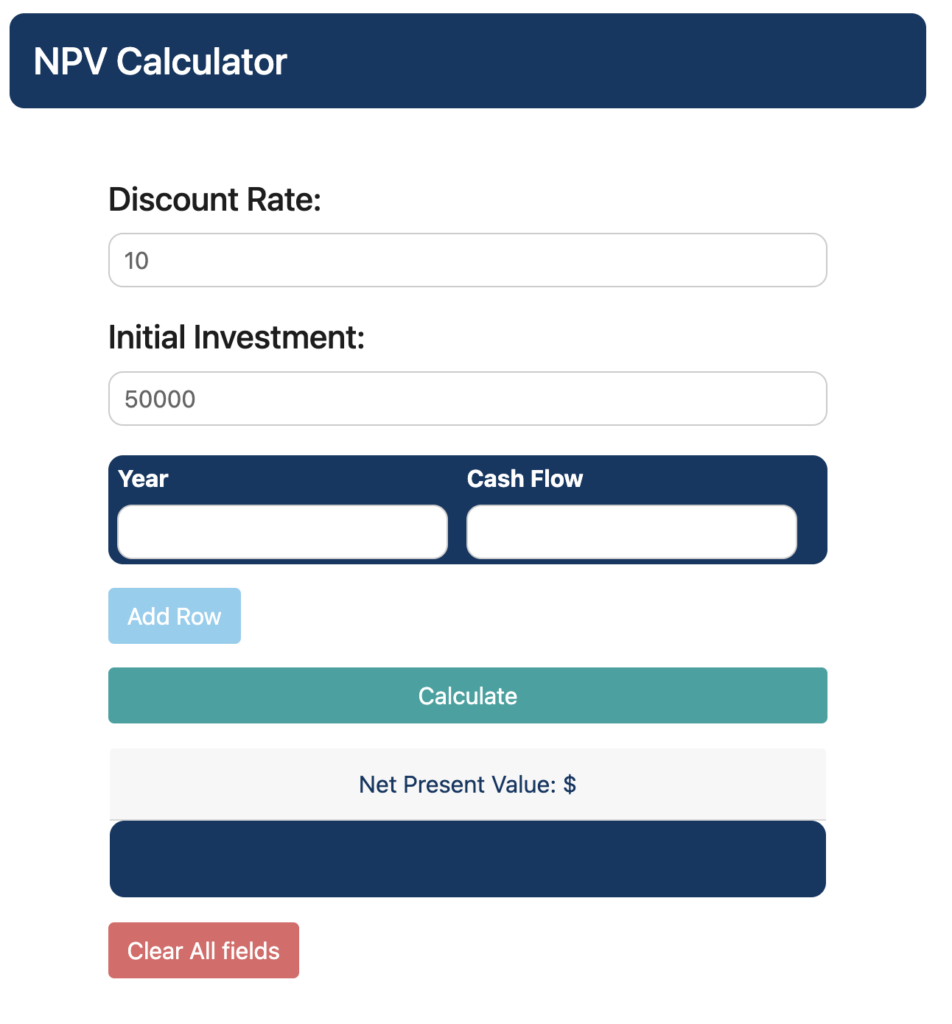
Step 2. Fill in the basic details, such as Discount Rate and Initial Investment.

For our project the initial investment is 50,000 and the discount rate is 10%. Please note that you do not have to input the $ sign, % sign or the separators.

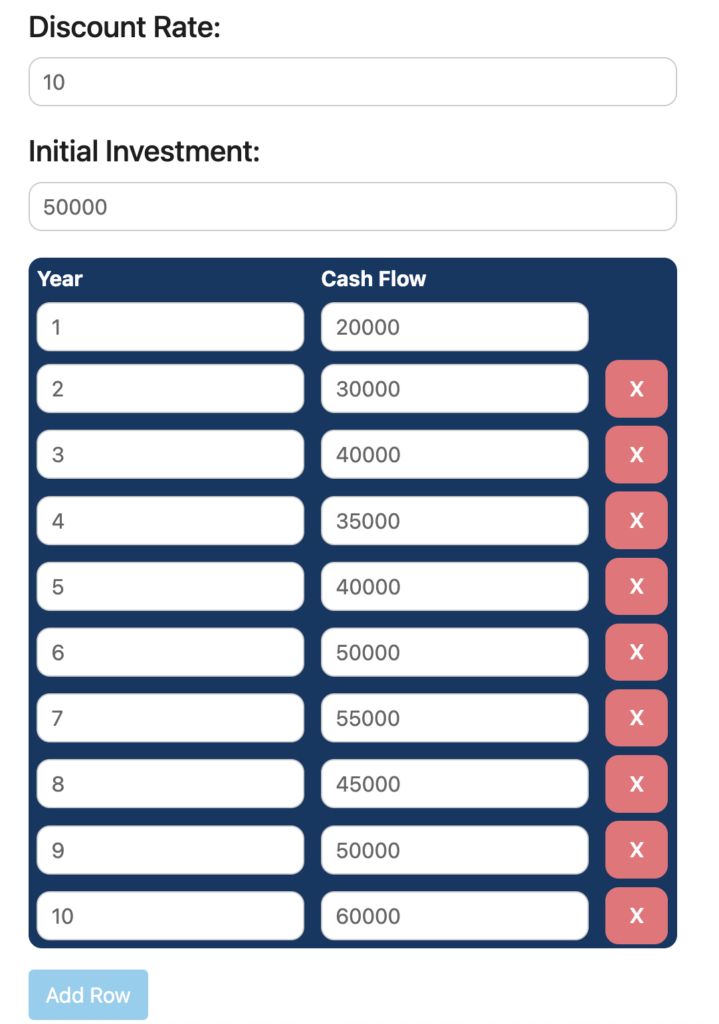
Step 3. Fill in the future years and the expected cash flows in the future years.

For our project, we are projecting future cash flows up to the next 10 years, so we can input the years and cash flows accordingly. More rows can be added easily by using the ‘Add Row’ button.

Step 4. Hit ‘Calculate’ To See Results

Once all the details are filled in, simply hit the ‘Calculate’ button to view results at the bottom of the page. In our case, the NPV of project comes out to be approximately $193,500.

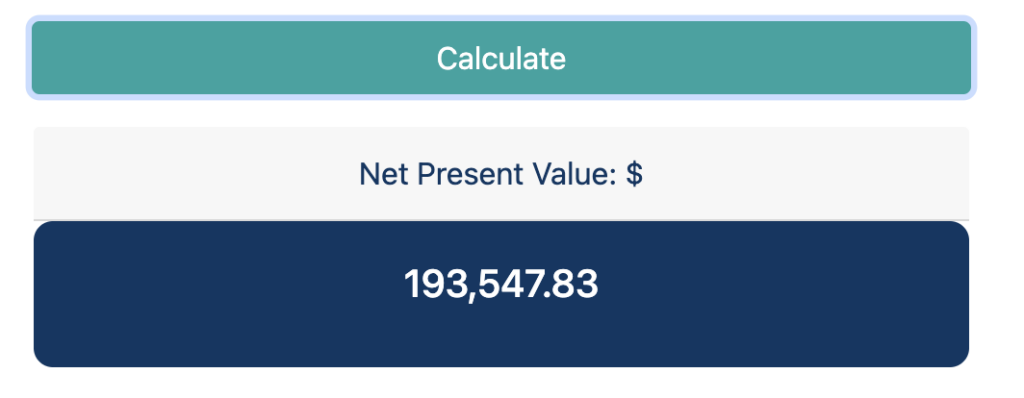
In our coffee shop example, the NPV of project would be: $193,548

(Sum of all present values = 243,548 [not shown in this calculation], initial investment = 50,000)

NPV = 243,548 – 50,000 = 193,548

Interpreting NPV Results

A positive NPV indicates that the project is expected to generate a return on investment (ROI) that exceeds the discount rate. This means that the project is worth pursuing financially. In our example, the NPV of $193,548 suggests that the coffee shop venture is a good project to pursue.

Conversely, a negative NPV would have indicated that the project is expected to generate an ROI below the discount rate. This means that the project should not be pursued as there are better investment opportunities available with the same investment amount and similar risks.

Conclusion

Net present value is a valuable tool for evaluating the profitability of investments or projects. By considering the present value of future cash flows and the discount rate, NPV helps decision-makers make informed choices about their financial ventures.